Light wings boost flight performance of tiny beetles.
Body size is correlated with flight speed. Miniature featherwing beetles can fly at three times their size. This performance results from a reduced wing mass and a previously unknown type of wing-motion cycle. The beetle Paratuposa placentis is one of the smallest insects, with a body length of 395 m. The flapping bristled wings follow a figure-of-eight loop that consists of subperpendicular up and down strokes followed by claps at stroke reversals above and below the body. The elytra act as brakes. Computational analyses suggest that the wingbeat cycle can be broken into two power half strokes, which produce a large upward force and two down-dragging recovery half strokes. The motion of bristled wings of the same size requires less power than heavier membranous wings. elastic energy storage is obsolete because of the positive mechanical power requirements. One of the factors of their evolutionary success is how small insects have preserved good aerial performance during miniaturization.
Miniaturization of various industrial products has been aided by scientific exploration of the smallest objects. Success stories of miniaturization are abundant in the living world. For more than 300 million years, ecological pressures have forced insects to develop extremely small bodies. Constraints that are insignificant at the macro scale become significant at the micro scale as the physical properties of flight depend on size. Flight at small sizes is dominated by air friction rather than force from the surrounding air. All animals that move through air have the same competition between inertia and friction that is important for flight.
Smaller insects fly slower than large insects. Some insects fly well. It was recently discovered that minute featherwing beetles are similar in speed to their larger relatives, despite a threefold difference in body length. The ptiliids can accelerate twice as fast as the carrion beetles. The peculiar structure of their wings and flight style is the reason for their excellent flight performance. The membranous wings of most insects are not the same as the feather-like bristled wings of Ptiliids. The modification of the flight apparatus evolved in small groups of insect orders. The benefits of ptiloptery have been largely unknown.
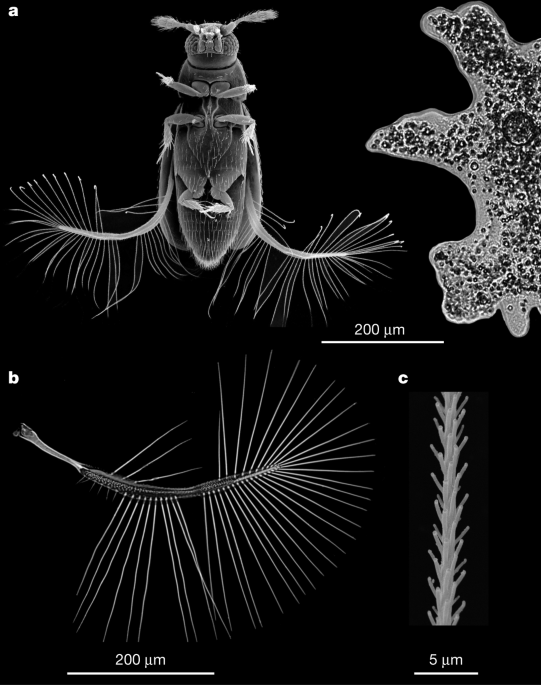
The External Morphology of P. placentis is shown in the first figure.
A wing of P. placentis and part of a seta are shown in the images.
Many studies have focused on the secrets of flight in minute insects, but most experimental data that reveal wing motion and aerodynamics have been obtained from larger insect species. Fruit flies, mosquitoes, and other millimetre-size insects have received a lot of attention in recent decades. The flow past evenly spacing cylinder lattices reduces aerodynamic force production in bristled wings according to two-dimensional numerical studies. Experiments with mechanical comb-like models suggested a slightly larger lift-to-drag ratio during the clap-and-fling phase in bristled wings compared with membranous wings17,18,19, but did not cover the full wingbeat cycle. It has become clear that small insects use a wingbeat cycle that is different from the larger ones, but, to our knowledge, the role of ptiloptery in this cycle has not been considered.
We analysed the flight of the miniature featherwing beetle. We constructed a model using data from light, confocal and electron microscopy, a kinematical model using synchronized high-speed videography, and a model using computational methods of solid and fluid mechanics. The combination of these methods gives a comprehensive view of how bristled wings work and explains why flying insects have bristled rather than membranous wings.
The smallest non-parasitic insect is P. placentis, with a body length of about 395 21 m. This size is similar to the size of some unicellular protists. The body mass of P. placentis is 2.43 0.19 g. The bristled wing has a petiole, a narrow wing blade and a fringe of setae. The setae occupy less than 1% of the aerodynamically effective wing area, which is 493 18 m.
Thematics of P. placentis.
A frame sequence of a single stroke in two projections.
The wingbeat cycle of P. placentis consists of two power strokes and two recovery strokes with wings clapping above and below the body. The Ptiliidae has unique recovery strokes that are different from the clap-and-fling motions used in other insects. The wings don't always clap at the end of the recovery stroke, depending on flight conditions. During the fling phases of the recovery strokes, the setal fringes of the left and right wings may intersect. The downstroke and upstroke have the same angle of attack, which is 73 during the downstroke and 85 during the upstroke. The cycle-averaged Reynolds number is 9 and reaches 20 during power strokes when wing velocity is highest. The increased AoA during power strokes and the presence of recovery strokes are similar to the motion of the larvae of Artemia sp.20 with a Reynolds number of 10.
The paths of the wing tips are wide and rounded. The aerodynamic asymmetry between power and recovery strokes should be maximized. The AoA and wing velocity reach their maxima after each power stroke. The peaks of forces and velocities are synchronized. 3d and 2f. The wing first produces an upward force as it quickly moves with net downward displacement and a small downward force while slowly moving edge-on upwards. The near-clap motion reduces the downward force on the parasites. The horizontal force on the wing is shown in a diagram. Positive peaks are greater due to drag than they are due to lift. The drag-based vertical force is accompanied by extended times. The simulation shows a pair of strong rings that are typical for drag-produced bodies. The beetle benefits from both drag and lift, as 32% of the cycle-averaged vertical force results from drag. The beetle has an estimated body mass of 2.4 g and a vertical acceleration of 1.0 m s2. The net contribution of the body and elytra to the force is insignificant.
There are forces on the wings of P. placentis.
The direction of total vertical force is shown in red and green. The posture at t/T of 0.6 is red and the posture at t/T of 0.82 is green. The arrows show aerodynamic force, wingtip velocity, yellow discs and arrows show surface orientation of the wing, and the arrows show time instants. The lines and arrows correspond to the right and left wing. The time span of power strokes is highlighted in yellow. The positive direction is nose down.
The large horizontal and vertical excursion of the wings during flapping poses a peculiar flight dynamics problem. The forces are small during the recovery strokes, but the arm relative to the centre of mass is large. This results in a pitching moment large enough to overturn the body around its pitching axis. The insect opens and closes the elytra with large waves compared to other flying beetles. The figures show that the elytra act as an insturment brake. Between t/T of 0 and 0.3, the wings are raised in a dorsal position and produce nose-up Torque. The elytra close causes a nose-down recoil on the body when the wings start their downstroke. The elytra decelerates and reopens when the wings produce nose-down Torque. The elytra movements decrease the amplitude of body-pitching by 50% compared with flight without elytra. The ptiliid beetles flying at high wingbeats are unique to their flying style and are likely to be the cause of the inertial brake observed in P. placentis.
The wing mass in P. placentis is about 1% of the body mass. Estimates of the mass of a membranous wing with the same outline amount to 0.13 or 0.18 g are different depending on wing thickness. The estimates were based on the smallest of the membranous-winged insects. The Ptiliidae and L. atomus are related. The bristled wing has a maximum entry of 1,600 g m2, while the membranous wings have a maximum entry of 16,000 and 20,800 g m2, respectively. The Ptiliidae wings have unique secondary outgrowths that reduce the wing mass by 44% compared with the bristled wing model with smooth cylindrical bristles at the same drag25. The bristled wing architecture with secondary outgrowths reduces wing mass compared to a membranous architecture. The conclusion is supported by an allometric analysis of wing mass in insects.
The bristled wing of P. placentis produces more vertical force than the membranous wing. The peaks in the mechanical power required for wing actuation are similar to those produced by the vertical force peaks. The average cycle-averaged power consumption in P. placentis is 28 W per kilogram of body mass, but instantaneous power can reach up to 120 W at t/T. The total mechanical power of the bristled wing model is positive during the entire wingbeat cycle because of the low inertia of the wing. There is no need for elastic energy storage. The aerodynamic power is similar to the membranous wing's in peak magnitude. The minimum mechanical power of the wing is 37 W and the peak power is 180 W. The Supplementary Information includes aerodynamic added mass effects during wing motion.
In generating aerodynamic force, impermeable membranous wings barely beat leaking bristled wings. The small advantage of using a membranous wing is overweighed by the advantage gained by reducing wing mass. This trade-off of energy savings for a small penalty in aerodynamic force generation is only available at Reynolds numbers of 10 or lower, where sufficiently low leakiness can be achieved with a small number of slender bristles.
Our understanding of the flight mechanics at low Reynolds numbers has been expanded by the findings reported here. In flight, small insects need to produce forces to support their body weight. The potential cost of an increase in power requirements is what P. placentis uses to maximize wing flapping amplitude. ptiloptery is an effective structural architecture that helps to reduce the costs of wing flapping, making elastic energy storage obsolete and reducing peak mechanical power requirements of the flight muscles. Power and slow-recovery strokes are part of the wingbeat cycle. The high-amplitude body pitch is caused by the wings. Inertial braking is an ingenious solution to this problem, enhancing posture stability without providing additional forces for flight. These mechanisms improve the temporal distribution of muscle mechanical power requirements and help to maintain aerial performance at an extremely small body size in P. placentis. Miniature beetles have a flight style that may explain their worldwide abundance. The convergent evolution of ptiloptery will be revealed by further studies of other microinsects with bristled wings.
Statistical methods were not used to determine sample sizes. The experiments were not randomized and the investigators were not blinded.
There is a material.
The adult featherwing beetles were collected in Vietnam. The beetles were collected and delivered to the laboratory. High-speed video recordings were made on the same day.
Morphology and morphometry are related.
The material for the studies was either alcoholic or alcohol based. After dehydration of the samples and critical point drying, the wing structure was studied using a scanning electron microscope. The samples were clarified with the help of a confocal microscope and a transmitted light microscope. Digital photographs were taken in ten different replications. Three-dimensional reconstructions were used to calculate body weights and weights of body parts.
There are moments of inertia and wing mass.
CLSM image-based models were used to measure the volumes of the wing's membranous part. The cuticle density was assumed to be 1,200 kg m3. The wing mass was obtained by summing up the contributions. To calculate the mass of the setae, we first estimated their linear density using a three-dimensional model. The blade of the wing model has no veins. The range of the membrane thickness was determined by the measurement of T. telengai, O. atomus and L. atomus. The values are the smallest measured in each species. The microscope was used to perform the measurements. The measurement error of linear dimensions is 1% in the spanwise direction and 10% in the thickness. The s.d. of the wing is 100 km. The root sum square error of the wing mass calculation is thought to be around 13%. The surface density of the membranous parts and the linear density of the bristles were calculated to evaluate the moments of inertia. The times of inertia of the individual setae were calculated using the formula for a thin rod at an angle. The moments of inertia of the membranous parts were calculated using a two-dimensional quadrature rule.
A high-speed recording.
The flight of the beetles was recorded in closed 20 20 20mm chambers, which were made of 1.0mm thick slides and 0.15mm cover-glass, and were illuminated by visible light. There were insects in the flight chamber. An air fan from the outside chilled the flight chamber. The temperature of the flight chamber was 22–26 C, while the ambient temperature was 22– 24 C.
The Evercam cameras were synchronized with a shutter speed of 20 s and a Frequency of 3,845 FPS. The high-speed cameras were mounted on optical rails and were positioned from the horizon. Two IR lights were placed next to the cameras and one above the flight chamber. There is a graphical representation of the setup in the previous study.
There is a measurement of kinematics.
13 recordings were selected for analysis. The flight of the PP2, PP4, PP5 and PP12 were similar to conventional hovering and we reconstructed the body parts in four cycles for each. The membranous wing model was used in the analysis of the PP2 kinematics. It is convenient to compare the performance of bristled wings with substitute membranous wings because it guarantees that the latter do not intersect. The tips of the bristles connect the lines that form the perimeter. The results obtained for individual PP2 are referred to in the descriptions and illustrations. Supplementary information and extended data figs can be found for the results obtained for other specimen. 2, 4 and 6.
The mean of the wingbeat Frequency was calculated. The number of frames was counted in several complete cycles.
The location of the insect's body parts were reconstructed using the Euler angles system. Three-dimensional models of the body and elytra were obtained by confocal microscope image stacking, and the flat wing model was based on light microscopy photos of dissected wings. The rigid flat wing model was used for the reconstruction of the kinematics. Frame sequences with four full kinematical cycles were prepared first. The frames were placed as projections between the bases of the wings. Virtual models of body parts were placed into a coordinate system. We manually changed the position and rotation of the body parts. A coordinate system was created for calculating the angles. The X0Y plane is a plane parallel to the stroke plane that intersects with the base of wing or elytron in the zero point. The major axis trend line of the wingtip coordinates is different from the linear trend line because it forms a wide scatter plot. The coordinates of the base and apex were used to calculate the stroke deviation angle. The angle between the stroke plane and the chord is called the pitch angle. The body pitch angle is the angle between the stroke plane and the longitudinal axis of the body. The angle of the stroke plane relative to the horizon was also measured.
Tracking the centre of the body in both projections and calculating the instantaneous velocity and its vertical and horizontal components in each frame was done for flight speed analysis. The obtained speed values were used to calculate the R package. The minimum distance between the wingblade tips was calculated.
Computational fluid dynamics.
Intervals of low-speed flight with duration longer than four wing beats were selected. The body angle, left wing, right wing, and elytra were all mapped on a uniform grid with a time step of 2.6 106 s. The data for each of the four cycles on a grid was computed by using the formula t with respect to t. The plots were shown in fig. The time average values of the loess-filtered time series were used to prescribe constant forward and upward/downward flight velocity.
The computational fluid dynamics analysis was performed using the open-source Navier–Stokes solver, which is based on the artificial compressibility method to enforce velocity-pressure coupling, volume penalization method to model the no-slip condition at the solid surfaces, and dynamic grid adaptation. The body of the flying insect is made of five rigid solid moving parts, the two elytra and the two wings moving relative to the body. Supplementary Information and Extended Data describes the protocol. The computational domain is a 12R 12R 12R cube, where R is the wing length, with volume penalization used in combination with periodic external boundary conditions to enforce the desired far-field velocity. The blocks contained 25 25 25 grid points. The blocks were redistributed among parallel computation processes so as to ensure the highest level of refinement near the solid boundaries and constant wavelet coefficients. The numerical simulations started from the quiescent air condition and continued for a time period of two wingbeat cycles with a coarse spatial grid resolution of xmin. The air temperature was 25 C in all cases, with a density of 1.197 kg m3 and an artificial speed of sound of 1.54 105 m2 s. Supplementary Information contains the volume penalization and other case-specific parameters. Supplementary Information and Extended Data discuss the accuracy of the simulation.
The aerodynamic force of a wing is reduced.
The drag component of the instantaneous aerodynamic force acting on the wing is defined as its projection on the direction of the wing velocity at the radius of gyration. The lift component is defined as subtracting the drag component from the total force. The time courses shown in fig. 3d are obtained from the total lift and drag force projected on the vertical direction.
A summary of the report.
The Nature Research Reporting Summary contains further information on research design.
The Open Science Framework repository has extended data sets and raw data.
Computational fluid dynamics simulations were performed using an open-source code, which can be downloaded from GitHub and has been described in detail elsewhere.
1.
The Simple Science of Flight: From Insects to Jumbo Jets was published in 2009.
2.
The flight performance of the smallest beetles. Proc. The National Acad. There is a science. USA 117, 24643– 24645.
The article is about a scholar.
3.
The features of the smallest insects and limits to miniaturization are what makes A. A. Small beautiful. Annu. Rev. Entomol. 60, 103–121
The article is about a scholar.
4.
In Living Machines: A Handbook of Research in Biomimetic and Bio hybrid Systems, Fukuda, Nakajima, M., Takeuchi, M. and Hasegawa, Y. Oxford Univ. The press, 2018).
5.
The skeletomuscular system of the smallest beetle, the Nephanes titan, has been studied. There is a tool called the Arthropods Struct. There is a person named Dev. 48, 71, and 82 were published in 2019.
There is an article about a scholar.
6.
The flight of insects. Nature 178, 1334–1335.
There is an article about a scholar.
7.
Sane and S. P. studied flight in miniature insects. It's a word. Opin. The brain is called aneurobiol. There were 41, 158, and 166 in this year's edition.
The article is about a scholar.
There are 8.
Estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Exp. There is a Biol. 59, 169, and 230 were written in 1973.
There is an article about a scholar.
There are 9.
Alap and fling mechanism with interacting porous wings in insect flight. J. Exp. There is a Biol. There were 217, 3898, and 3909 in this year.
There is a scholar named PubMed.
10.
A novel wing flapping and drag principle is used by insects. J. fluid Mech.
There is an article about a scholar.
11.
Flapping-mode changes and aerodynamic mechanisms in insects. It's called Phys. Rev. E 99 was published in 2019.
The article is about a scholar.
There are 12.
The aerodynamic basis of insect right and wing rotation were studied. Science 284 was published in 1999.
The article is about a scholar.
13
The control of free flight in flies. There is a word for that. Trans. R. Soc. B 372, 20150388
There is an article about a scholar.
There are 14.
Bomphrey, Nakata, T., Phillips, N. and Walker were involved in the research. Nature 541, 92–95
The article is about a scholar.
15.
A bristled wing has an Aerodynamic Characteristics of Unstable Gap Flow in it. It's called Phys. Fluids 30-071901.
There is an article about a scholar.
16.
Optimal configuration of a two-dimensional bristled wing. J. fluid Mech. The A23 will be numbered in 2020.
There is an article about a scholar.
17
V. T., Terrill, C. L., Ford, M. P., and Santhanakrishnan were involved in the study. Fluids 3 and 44 were published in the same year.
There is an article about a scholar.
18.
Aerodynamic interaction of bristled wing pairs. It's called Phys. There are fluids 33 and 3 in this year's edition of Fluids.
The article is about a scholar.
19
Ford, M. P., Kasoju, V. T., Gaddam, M. G., and Santhanakrishnan, A. There is a person named Bioinspir. There is a person named Biomim. There are 14 articles in this edition.
There is an article about a scholar.
20.
Physical constraints on the design of oscillating wings, fins, legs, and feet at intermediate Reynolds numbers are the subject of functional morphology and virtual models. Integr. Comp. There is a Biol. There were 42, 232, and 243 in 2002.
There is an article about a scholar.
21.
The clap-and-fling mechanism in small wasp Encarsia formosa was studied by Cheng, X. and Sun, M. It's called Phys. Fluids 31 was published in 2019.
22.
The role of elytra in beetle flight. J. Bionic Eng.7 was published in 2010.
There is an article about a scholar.
There is a new date for this.
A numerical and theoretical study of the aerodynamic performance of a hovering rhinoceros beetle. J. fluid Mech. 884, A18
The article is about a scholar.
24.
The flight, wing movements and wing structure of the male Priacma serrata were observed by D. M. Cupedidae is aColeoptera. Can. Entomol is a drug. 90, 341, 347.
There is an article about a scholar.
25.
Aerodynamic performance of a bristled wing of a very small insect is studied using a revolving wing model. Exp. Fluids 61,194 were published in 2020.
The article is about a scholar.
26.
There are features associated with miniaturization and functional scaling analysis in featherwing beetles. There is a tool called the Arthropods Struct. There is a person named Dev. 48, 56, and 70 were published in 2019.
There is an article about a scholar.
27.
Design and mechanical properties of insects. There is a tool called the Arthropods Struct. There is a person named Dev. 33, 187–199 were published in 2004.
There is an article about a scholar.
There is a new date for this.
The aerodynamics of hovering insect flight. I. Thematics. There is a word for that. Trans. R. Soc. B 305 was published in 1984.
A scholar from the internet.
29.
Cheng, X. and Sun, M. Wing-kinematics were used in a hovering insect. There is a science. Rep. 6, 25706.
The article is about a scholar.
30.
T., Schneider, K., Reiss, J., and Farge are authors. M is a wavelet-adaptive method for multiscale simulation of turbulent flows. Commun. Comput. It's called Phys. The year of 1118–1149.
The article is about a scholar.
References can be downloaded.
A.A.P. thanks R. D. Zhantiev for inspiring him to study insects. We would like to thank A. K. Tsaturyan. The Russian Science Foundation supported the work of S.E.F., A.A.P., P.N.P. and N.A.L. The study was done using equipment of the shared research facilities of the high performance computing resources at the Moscow State University. The work of D.K. was supported by a grant. The grant number 19H02060 was partially supported by H.L. The contributions of F.-O.L. and T.E. were supported by grants. Three-dimensional electron microscopy and spectroscopy was used in the studies.
The authors do not have competing interests.
Nature thanks Michael Dickinson, Adrian Thomas and the other anonymous reviewer for their contribution to the peer review of this work. There are peer reviewer reports available.
The data points for living mass of membranous insect wings are shown in filled circles. The dried mass of membranous wings of Staphylinoidea beetles can be seen in circles. The weight of the bristled wing of the featherwing beetle is shown by the cross. The mass range of membranous wings is estimated. The blue dashed line is an allometric trend based on the data for membranous wings. Data for dried wings of Staphylinoidea is used to create the orange dashed line. The data show the mass and area of one wing in Coleoptera and Diptera.
There are wings and elytra with body pitch angle and vertical and horizontal components of body acceleration.
Time instances are t/T, t/T, t/T, and t/T from top to bottom.
The aerodynamic force on the insect is broken down into the horizontal and vertical components.
A, PP2, b, PP4, c, PP5. Supplementary fig. 9 has an interactive 3D PDF version.
The mechanical power is positive through the entire wingbeat cycle period. The contribution from the air is very strong.
Positive direction is nose down.
Mass-specific aerodynamic power is the Aerodynamic force.
The vertical force coefficients in three different species have different time variations. The data for the large rhinoceros beetle Trypoxylus dichotomus and for the tiny chalcid wasp Encarsia formosa are adapted so that the cycle begins with the downstroke. The force coefficients are 2FV/ (2Rgf)2S, where FV is vertical force, is air density, is flapping amplitude, Rg is wing geometric radius of gyration, f is flapping Frequency, and S is wing area. The bristled wings of Encarsia formosa were modeled after impermeable solid plates. For more information, see the Supplementary Information.
Body-mass-specific mechanical power can be varied by time and peak.
Supplementary Sections 1–19 are included in this file. Supplementary Tables 1–4.
The flight of P. placentis PP2. Videos are projected in two different ways.
The flight of P. placentis PP4. Videos are projected in two different ways.
The flight of P. placentis PP5. Videos are projected in two different ways.
The flight of P. placentis. Videos are projected in two different ways.
The P. placentis PP2 model is being rendered in a computer. The rendering of the model used for CFD is in the top left corner. The model is the same in the top projection. In the left and right are the iso-surfaces of the vorticity magnitude. The axes x, y and Z are shown in red, yellow and green.
The P. placentis PP5 model is being rendered in a computer. The rendering of the model used for CFD is in the top left corner. The model is the same in the top projection. In the left and right are the iso-surfaces of the vorticity magnitude. The axes x, y and Z are shown in red, yellow and green.
You agree to abide by the Community Guidelines if you submit a comment. If you find something that does not comply with our guidelines, please flag it as inappropriate.
We use cookies to make sure that our website works properly, as well as some optional cookies to personalize content and advertising, provide social media features and analyse how people use our site. Some countries outside of the European Economic Area do not have the same data protection standards as the country where you live, so if you accept some or all optional cookies, you give consent to the processing of your personal data, including transfer to third parties. Clicking on 'Manage settings' will show you more information about how your personal data is processed. Further information can be found in our privacy policy.
Page 2
A wing of P. placentis and part of a seta are shown in the images.