Advancing mathematics by using artificial intelligence.
Alex Davies orcid.org/0000-0003-4917-5341.
Petar Velikovi1.
The person is Lars Buesing.
Sam Blackwell.
The person is Daniel Zheng.
Nenad Tomaev orcid.org/0000-0003-1624-02201.
Richard Tanburn.
Peter Battaglia.
Charles Blundell1.
Andrs Juhsz2.
There is a man named Lackenby2.
The person is Geordie Williamson.
...
The orcid.org/0000-0003-2812-99171 contains information about the person.
Pushmeet Kohli is at orcid.org.
This article is about Nature 600*, 70–74.
The practice of mathematics involves discovering patterns and using them to form and prove hypotheses. The Birch and Swinnerton-Dyer conjecture is one of the most well-known examples of the use of computers in mathematics. Here we show examples of new fundamental results in pure mathematics that have been discovered with the assistance of machine learning. We propose a process of using machine learning to discover potential patterns and relations between mathematical objects, understanding them with attribution techniques and using these observations to guide intuition and propose conjectures. In each case, we show how the machine-learning-guided framework led to meaningful mathematical contributions on important open problems, such as a new connection between the algebraic and geometric structure of knots. Our work may serve as a model for collaboration between the fields of mathematics and artificial intelligence that can achieve surprising results by using the strengths of mathematicians and machine learning.
One of the main drivers of mathematical progress is the discovery of patterns and the creation of useful conjectures, statements that are suspected to be true but have not been proven to hold in all cases. Data has always been used to help in this process, from the early hand-calculated prime tables used by Gauss and others to the modern computer-generated data used in the Birch and Swinnerton-Dyer conjecture. Computational techniques have become more useful in other parts of the mathematical process, but artificial intelligence systems have not yet established a similar place. Prior systems for generating conjectures have contributed useful research by using methods that are not easy to generalize to other mathematical areas, or have demonstrated novel, general methods for finding conjectures that have not yet yielded useful results.
Artificial intelligence, in particular the field of machine learning, offers a collection of techniques that can effectively detect patterns in data and has become a utility in scientific disciplines. Artificial intelligence can be used in mathematics to find counterexamples to existing conjectures, accelerate calculations, generate symbolic solutions and detect the existence of structure in mathematical objects. In this work, we show that artificial intelligence can be used to assist in the discovery of mathematics. This extends work by using supervised learning to find patterns and enable mathematicians to understand the learned functions. We propose a framework for augmenting the standard mathematician's toolkit with powerful pattern recognition and interpretation methods from machine learning and demonstrate its value and generality by showing how it led to two fundamental new discoveries. Our contribution shows how mature machine learning methodologies can be integrated into existing mathematical workflows to achieve novel results.
It is only with a combination of both rigorous formalism and good intuition that one can tackle complex mathematical problems. The framework shows how mathematicians can use machine learning to help them understand mathematical relationships and how they can use machine learning to guide their intuitions. This is a natural and productive way that these well-understood techniques in statistics and machine learning can be used in a mathematician's work.
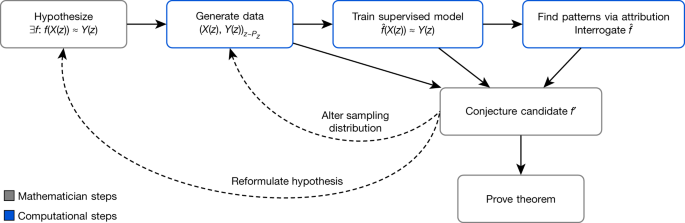
The framework is depicted in fig. 1.
A machine learning model is trained to estimate a function over a particular distribution of data PZ, which helps guide a mathematician's intuition. The insights from the accuracy of the learned function can help in understanding the problem and the construction of a closed-form f. The process is iterative and interactive.
It helps guide a mathematician's intuition about the relationship between two mathematical objects X(z) and Y(z) associated with Z. The number of edges and vertices of Z can be used as an example. There is an exact relationship between X(z) and Y(z) in this case, according to the formula. The relationship could be rediscovered by using traditional methods of data-driven conjecture generation. This approach is less useful for X(z) and Y(z) in higher-dimensional spaces, or for more complex types, such as graphs.
The framework helps guide the intuition of mathematicians by helping to verify the existence of structure/patterns in mathematical objects through the use of supervised machine learning, and by helping to understand these patterns through the use of attribution techniques.
The mathematician proposes a hypothesis that there is a relationship between X and Y. We can use supervised learning to train a function that predicts Y(z) using only X(z) as input. The broad set of possible nonlinear functions that can be learned from a sufficient amount of data are the key contributions of machine learning in this regression process. If (hatf) is more accurate than would be expected, it means there may be a relationship to explore. Attribution techniques can help the mathematician understand the learned function (hatf) sufficiently for him to guess a candidate f Attribution techniques can be used to understand which aspects of (hatf) are relevant for predictions. Many techniques aim to quantify which component of the function is sensitive to. The method we use to calculate the derivative of outputs of (hatf)) with respect to the inputs is called the gradient saliency. This allows a mathematician to look at the problem in a different way. This process might need to be repeated several times. The mathematician can guide the choice of conjectures to those that are plausibly true and suggestive of a proof strategy.
This framework provides a test bed for intuition, which can be used to verify whether an intuition about the relationship between two quantities is worth pursuing and, if so, guidance as to how they may be related. We used the above framework to help mathematicians get results in two cases, one of which was the discovery and proving of a relationship between a pair of invariants in knot theory. The framework helped guide the mathematician to achieve the result. The models can be trained on a single graphics processing unit in each case.
The low-dimensional area of mathematics is influential. One of the key objects that are studied is the knot, which is a simple closed curve, and the subject's main goals are to classify them, to understand their properties and to establish connections with other fields. One of the ways that this is done is through invariants, which are the same for any two equivalent knots. There are many different ways in which these invariants are derived. These two types of invariants are derived from different mathematical disciplines, and so it is of great interest to establish connections between them. There are some examples of invariants for small knots shown in the second figure. A notable example of a conjectured connection is the volume conjecture26, which proposes that the hyperbolic volume of a knot should be hidden within the coloured Jones polynomials.
There are invariants for three hyperbolic knots.
There was a previously undiscovered relationship between the geometric and algebraic invariants.
Our hypothesis was that there is a relationship between the hyperbolic and algebraic invariants of a knot. A supervised learning model was able to detect the existence of a pattern between a large set of geometric invariants and the signature (K), which was not previously known to be related to the hyperbolic geometry. The relationship between the three invariants of the cusp geometry was visualized partly in fig. 3b. A second model with X(z) consisting of only these measurements achieved a very similar accuracy, suggesting that they are a sufficient set of features to capture almost all of the effect of the geometry on the signature. The real and imaginary parts of the meridional and longitudinal translation were the three invariants. There is a relationship between the quantities and the signature. The relationship is best understood by means of a new quantity, which is related to the signature. The natural slope is defined as slope(K) + Re(/) where Re is the real part. It has a geometric interpretation. One can see the curve as a geodesic on the torus. It will return and hit at some point if one fires off a geodesic from this. It will have traveled along a longitude and a multiple of the meridian. The natural slope is the multiple. The endpoint of might not be the same as its starting point. Our initial hypothesis was about natural slope and signature.
The knot theory is attributed in fig. 3.
Attribution values for each input. The features with high values are those that the learned function is most sensitive to. There are 10 retrainings of the model and the 95% confidence interval error bars.
There are constants for every hyperbolic knot.
2sigma (K)-rmslope(K)
The edges were aggregated by their edge type and compared to the overall dataset. The effect on the edges was shown in the subgraphs for the higher-order terms.
Evaluation.
The threshold Ck was chosen as the 99th percentile of the values in the range 95, 99.5, although the results are present for different values of Ck in the range. The measure of edge attribution is visualized in the figure. We can confirm the pattern by looking at aggregate statistics over many runs of training the model, as shown in fig. 5b. The two-sided t-test statistics are as follows: simple edges: t is 25.7, P is 4.0, and the other is t is 13.8. The significance results are robust to different settings of the model.
There are notebooks that can be used to regenerate the results for knot theory and representation theory.
The generated datasets used in the experiments have been made available for download.
1.
Borwein and Bailey did a mathematics experiment.
2.
Birch and Swinnerton-Dyer wrote notes on elliptic curves. I. J. Reine Angew was a woman. There's a lot of math. The year 1965, 81–108.
The mathSciNet MAth is a scholarship.
3.
The Millennium Prize Problems were written by J. Carlson.
4.
F. Kazhdan-Lusztig polynomials are about history, problems, and invariance. Sémin. Lothar. There is a comb. B49b was published in 2002.
The mathSciNet MAth is a scholarship.
5.
Hoche wrote "In aedibus BG Teubneri, 1866"
6.
M. Khovanov wrote about patterns in knot cohomology. There's a lot of math. There were 12 in 2003
The article is about a scholar.
7.
The planar map is four colorable. The American Mathematical Society published 98 in 1989.
There are 8.
Half a year of the Liquid Tensor Experiment: amazing developments.
There are 9.
S. Fajtlowicz wrote in the Annals of Discrete Mathematics. Elsevier wrote about 38 113–118 in 1988.
10.
The DIMACS Series is about mathematics and computer science. The eds Fajtlowicz, S. et al. were published in 2005.
11.
Generated conjectures on fundamental constants with the machine. Nature 590, 67– 73, will be published in 2021.
The article is about a scholar.
There are 12.
Information Theory, Inference and Learning Algorithms was written by D. J. C. The press, 2003)
13
C. M. Bishop wrote about pattern recognition and machine learning.
There are 14.
LeCun, Bengio, Y., and Hinton are related. Nature
The article is about a scholar.
15.
A survey of deep learning. Preprint at arxiv.org/abs/2003.11755
16.
A Z. Wagner wrote about neural networks. The preprint is at https://arxiv.org/abs.
17
Peifer, Stillman, M. and Halpern-Leistner are studying selection strategies. Preprint at arXiv.org.
There is a new item on the market.
Deep learning for symbolic mathematics was written by Lample and Charton. Preprint at arXiv.org.
19
He is a machine-learning mathematical structures. The preprint is at https://arxiv.org/abs-2101.0617.
20.
Carifio, Halverson, J., and Nelson were involved in machine learning in the string landscape. J. High Energy Phys. The year was 2017: 157.
The article is about a scholar.
21.
Heal, K., Kulkarni, A., and Sertz, E. C. are researchers. There is a pre-print at this website.
There is a new date for this.
A neural network approach to predicting and computing knot invariants. Preprint at arXiv.org.
There is a new date for this.
Big data approaches to knot theory: understanding the structure of the Jones polynomial. Preprint at arXiv.org.
24.
Jejjala, V., Kar, A., and Parrikar, O. are learning hyperbolic volume of a knot. It's called Phys. Lett. B 799, 135033 were added to the list.
There is a article about mathSciNet and a article about the scholar.
25.
There is more to mathematics than proof and rigor.
There is a new date for 26.
The volume of knots from the quantum dilogarithm is hyperbolic. Lett. There's a lot of math. It's called Phys. 39, 269–275 was published in 1997.
The article is about a scholar.
27.
The signature and cusp geometry of hyperbolic knots. The print is in the press.
There is a new date for this.
Representation of Theory of Finite Groups and Associations. The American Mathematical Society was founded in 1966.
29.
F., Caselli, F., and M. are related. Adv. math. 202,555–604 was published in 2006
The article is about a scholar.
30.
The structure of certain representations of Lie algebras. Bull. Am. There's a lot of math. It's Soc. 74, 160–166 were released in 1968.
The article is about a scholar.
31.
From moment graphs to intersection cohomology by T. and R. There's a lot of math. Ann. There were 335, 533, and 541 in 2001.
The article is about a scholar.
There are 32.
The invariance for the Kazhdan-Lusztig polynomials was discussed. The print is in the press.
33.
The game of Go can be mastered with deep neural networks. Nature 484–489 was published in Nature.
The article is about a scholar.
34.
The man who knew the secret of the genius was named R. Kanigel.
35.
The Value of Science was written by Henri Poincaré.
36.
Hadamard wrote The Mathematician's Mind. The Press, 1997.
37.
M., Bruna, J., Cohen, T., and Velikovi are related. Preprint at the following website: http://arxiv.org/abs-2104.13478.
38.
M. A. in mathematical methods for digital computers.
39.
Neural image caption generation with visual attention is the topic of a paper by K. and others. In Proc. The International Conference on Machine Learning was held in 2015.
40.
M., Taly, A., and Q. are related to axiomatic attribution for deep networks. In Proc. The International Conference on Machine Learning took place in the year of 2017:
There are 41.
Bradbury, J. et al. JAX: composable transformations of Python+NumPy programs.
There are 42.
A. B. A. D. I. et al. are using machine learning on heterogeneous systems.
There are 43.
In Advances in Neural Information Processing Systems 32, A. et al.
44.
Three dimensional manifolds, Kleinian groups and hyperbolic geometry were written by W. P. Thurston. Bull. Am. There's a lot of math. The Soc 6, 358–381, was published in 1982.
The article is about a scholar.
45.
The geometry and topology of 3-manifolds is studied with the computer program, snappy.computop.org.
46.
The next 350 million knots. In Proc. The 36th International Symposium on Computational Geometry will be held in 2020.
There are 47 items.
The -coefficient of Lusztig polynomials is a class of equivalence. Exp. There's a lot of math. 20, 476–476.
The article is about a scholar.
48.
Neural message passing for quantum chemistry. Preprint at arXiv.org.
49.
The execution of graph algorithms is Neuralized. Preprint at arXiv.org.
References can be downloaded.
We appreciate the help and feedback from J. Ellenberg, S. Mohamed, O. Vinyals, A. Gaunt, A. Fawzi and D. Saxton. DeepMind funded this research.
The authors do not have competing interests.
A slope vs signature for a random dataset.
The table has accuracies for predicting KL coefficients from Bruhat intervals.
Supplementary text is in this file. hyperbolic knots and references.
You agree to abide by the Community Guidelines after submitting a comment. If you find something that does not comply with our guidelines, please flag it.
Cookies are used to store or retrieve information on any website. This information is used to make the site work as you expect it to, and it might be about you, your preferences or your device. The information can give you a more personalized web experience, but it doesn't usually identify you. We respect your right to privacy, so you can choose not to allow some cookies. Click on the different headings to find out more. blocking some types of cookies may affect the experience of the site and the services we can offer.
The website cannot function without these cookies. They are usually set in response to actions you take that are related to a request for services. Some parts of the site will not work if you block or alert your browser about these cookies. The cookies do not store any personally identifiable information.
We can measure and improve the performance of our site with the help of these cookies. They help us to know which pages are popular and which are not. All information collected by these cookies is anonymous. If you don't allow these cookies, we won't know when you have visited our site and we won't be able to monitor its performance.
Enhancements to the website can be provided by these cookies. They can be set by us or by third party providers. Some or all of the services may not work if you don't allow these cookies.
Our advertising partners may set these cookies on our site. They can be used to build a profile of your interests and to show you relevant ads on other sites. They do not store personal information, but are based on your browser and internet device. You will experience less targeted advertising if you don't allow these cookies.
The cookies are set by a range of social media services that we have added to the site to enable you to share our content with your friends and networks. They can track your browser and build up a profile of your interests. This may affect the content on other websites you visit. You may not be able to use or see the sharing tools if you don't allow these cookies.
Our site may be used to set these cookies. They can be used to build a profile of your interests and to show you relevant content. They do not store personal information, but are based on your browser and internet device. If you don't allow these cookies, you may experience less personalized content and advertising.
Our advertising partners may set these cookies on our site. They can be used to build a profile of your interests and to show you relevant ads on other sites. They do not store personal information, but are based on your browser and internet device. You will experience less targeted advertising if you don't allow these cookies.
Allowing third-party ad tracking and third-party ad serving through vendors. You can see more information on the ads.
We use cookies to make sure that our website works properly, as well as some "optional" cookies to personalize content and advertising, provide social media features and analyse how people use our site. If you accept cookies, you give consent to the processing of your personal data, including transfer to third parties, in countries that do not offer the same data protection standards as the country where you live. Clicking on "Manage Settings" will allow you to decide which optional cookies to accept.
