Imagine you are hosting a small party for six people and you don't know who they are or who they don't know. There will be at least three people who are strangers to each other and three who are already friends. We don't assume your friends don't like each other. There will always be at least one group of three people who are unknown to each other.
The more you think about the problem, the more fascinating it is. Six people have a lot of things in common. How does person A and person B relate to one another? A and C are related to one another. Is B aware of C? One of two values can be found in these connections. There are two different ways in which the partygoers can relate to one another. According to the math, there is always a trio of people in a group who know one another. Looking for a trio is rather difficult.
Frank Ramsey was a British mathematician who died at the age of 26. He was able to develop a branch of mathematics that deals with chaos. In the case of our partygoers, recurring patterns are the aim. There is at least one group of three people who all know one another or at least one group of three complete strangers.
graphs are networks of points and edges and can be used to solve the problem. There are people who symbolize a nodes. Six people can be in a circle. Each point has a connection. The edges are created by this. They are either red or blue depending on whether they know each other or not. The claim is that regardless of how you color the edges, you always get a triangle.
According to the Ramsey theory, no matter how you color the edges, you always get at least one all- blue or all- red figure. The triangle will always appear if you try.
People don't want to look through the possibilities. Ramsey wanted to know if six is the smallest number of guests that would inevitably form a triangle. Changing the number of people invited is a solution to this problem. There is proof to the contrary if you find triangles colored in a way so that they don't appear in a straight line. Two of the people could have met before you invited them. There isn't a trio of people who are all known to each other.
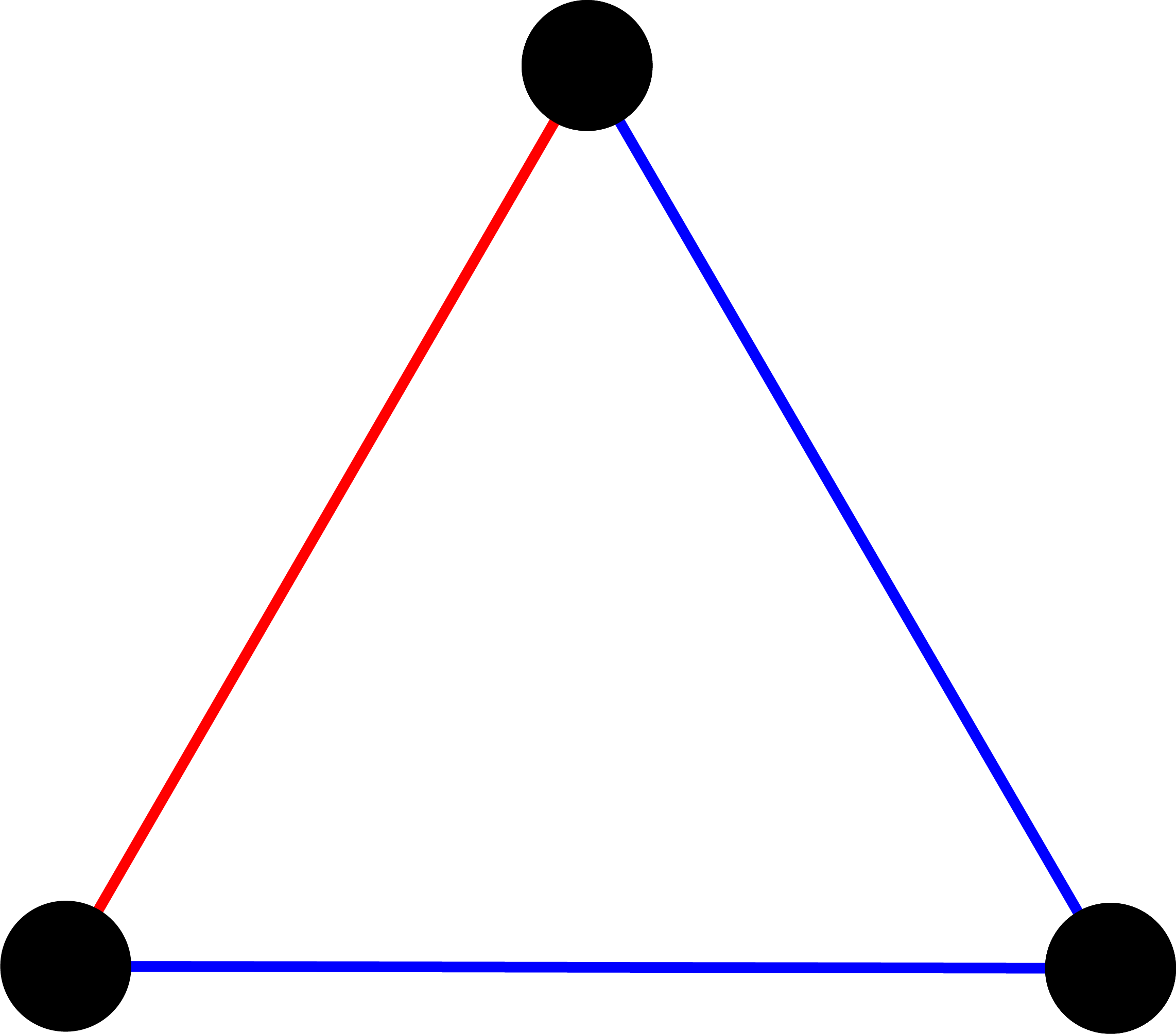
It is easy to find cases in which there is no group of three who are known to each other.
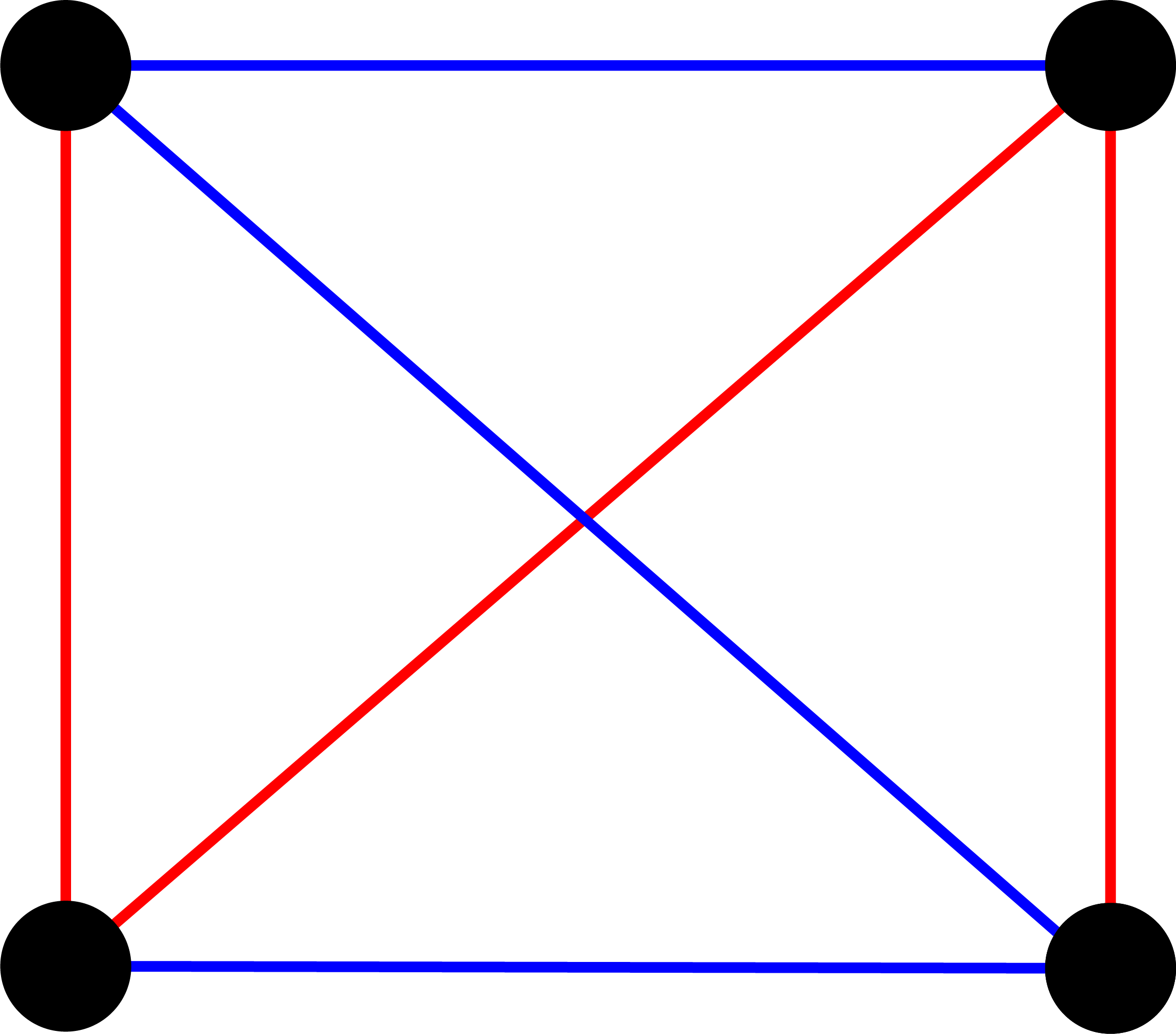
A triangle of the same color is not the only configuration of friend-stranger connections. The number must be more than five to answer Ramsey's question about the smallest group of partygoers. Is it more?
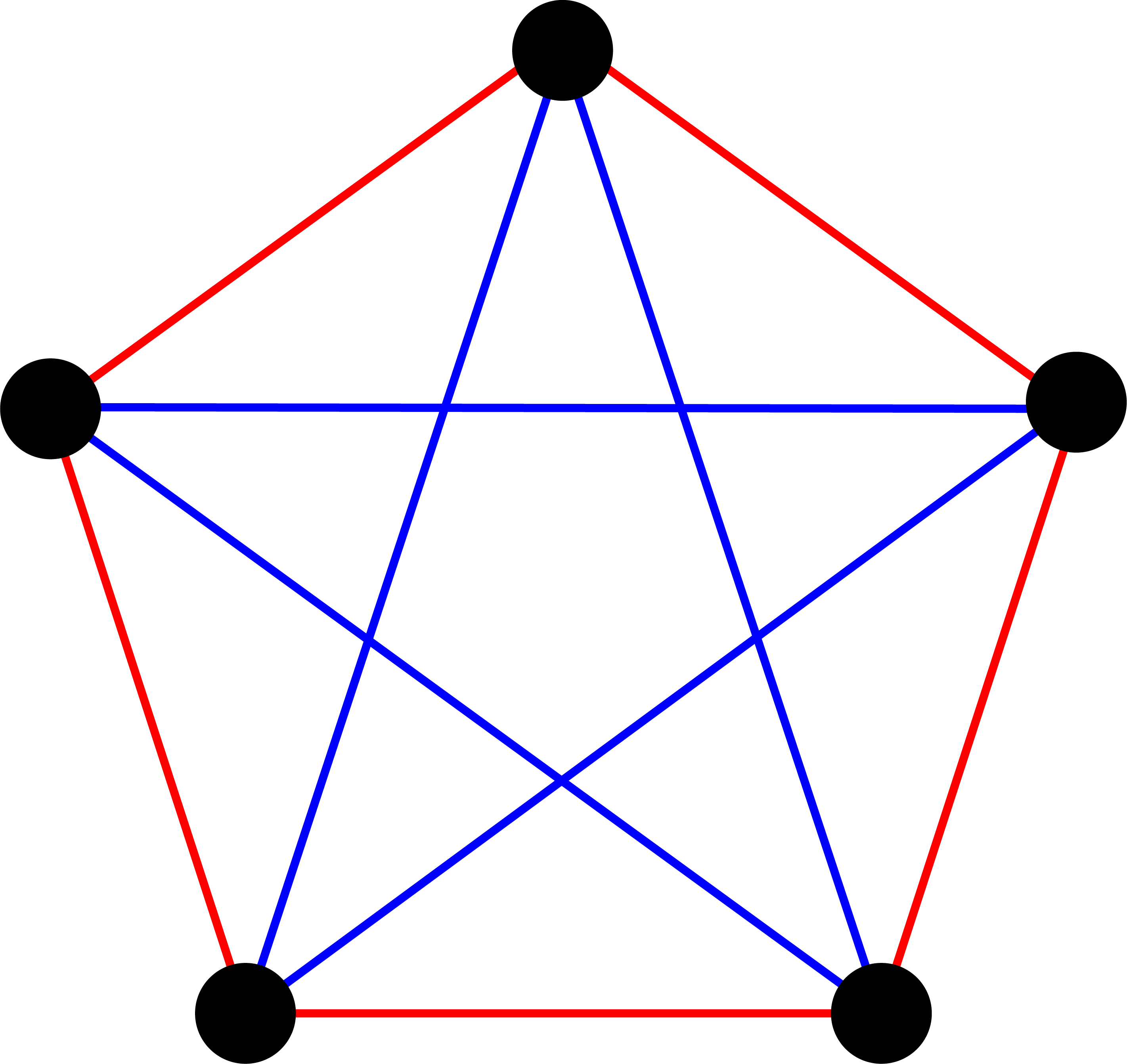
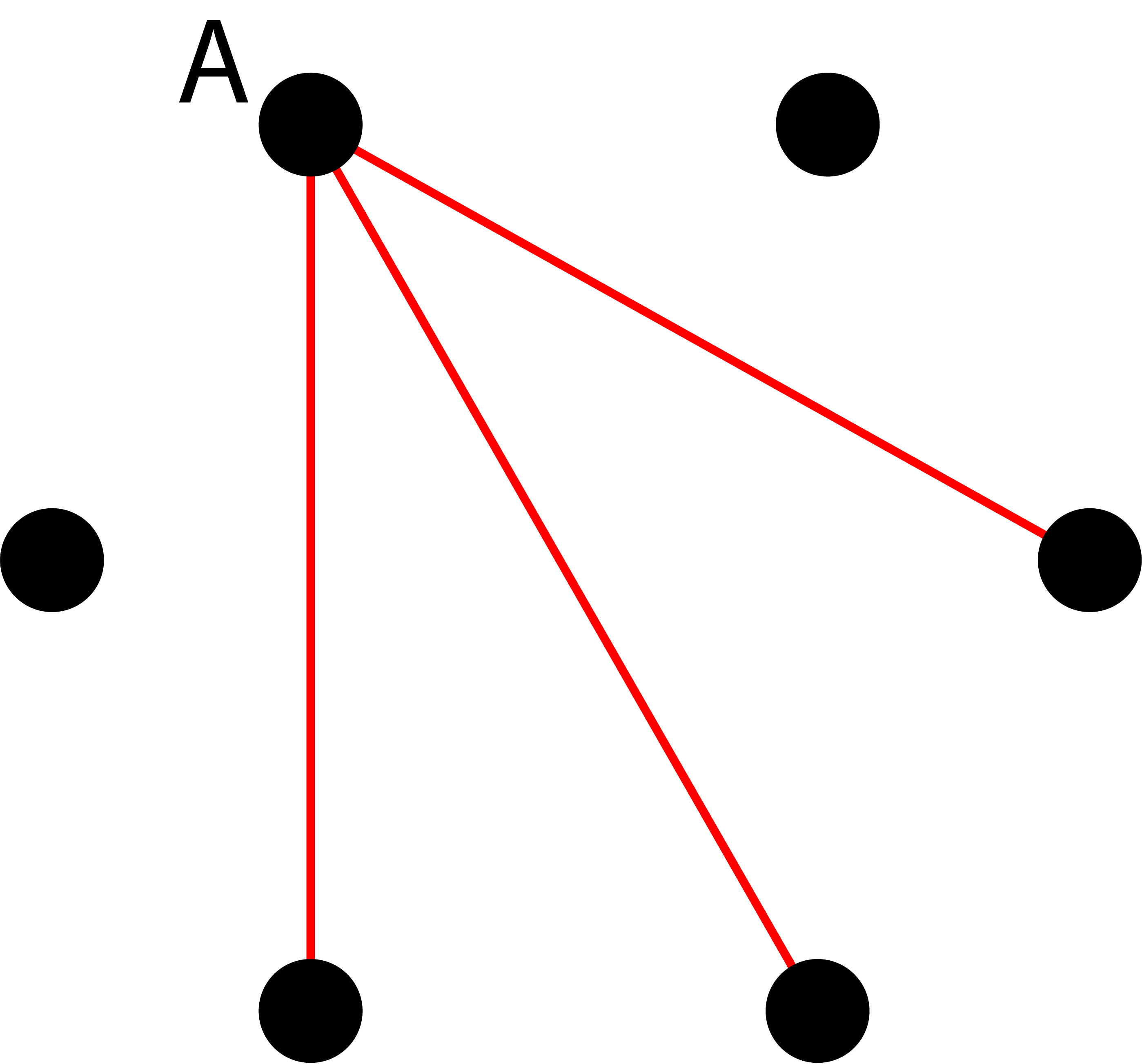
When we reach six people, what do we do? If you want to create a single-colored triangle, you need to color the edges of the graph. Pick out a single person A and look at their relationship to the other guests. Person A is the hostess. How many people do she have? There are six different ways in which she can connect with the five guests. There are four strangers in this scenario. Six partygoers might connect with the hostess in different ways.
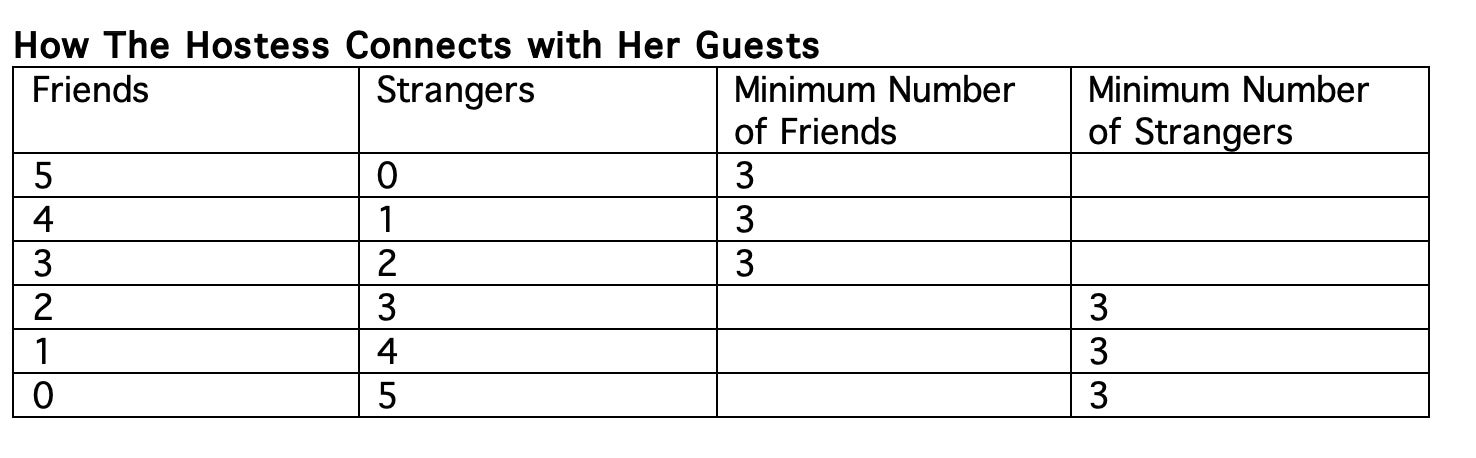
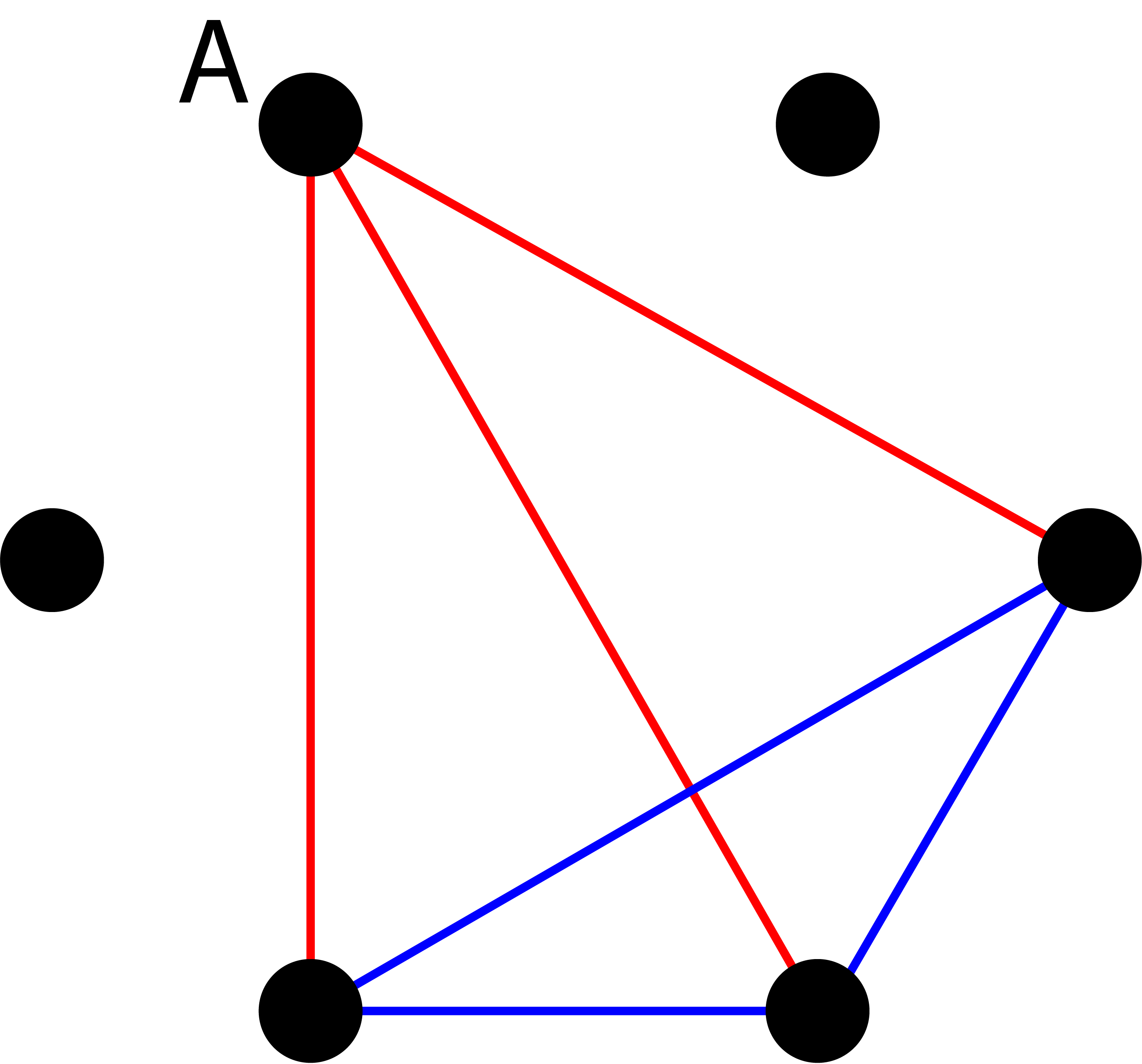
At least three people are known to the hostess. The graph shows that she has at least three edges of the same color. One can assume that in one of the configurations shown in the table, the hostess has three red edges, which means she knows three other people. You can try to avoid a red triangle by coloring the remaining connections in a way that avoids them.
It is necessary to make sure that any two people who know the hostess don't know each other. You get a blue triangle if you mark all the edges in blue. There is no way to avoid a single-color triangle in a six point graph. You can see a triangle in a larger graph. As soon as you invite more than five people, there will always be a group of three people who know each other or not.
You can sign up for Scientific American's newsletters.
Calculating a single result isn't enough for mathematicians. They try to find a solution. To get a general case for Ramsey numbers, they would ask, "What is the minimum number of nodes R needed to always find a red m-clique or a blue n-clique?" A n-clique is a group of points that are connected. The number is called the number. Most Ramsey numbers are unknown. We proved that R3 is 6. It is possible to show that R(4) is 18. If you invite 18 people to a party, there will always be a group of four who don't know each other.
For a long time, it has been unclear how large R is. What is the smallest number of people you need to invite so that there is always a group of people? We now know that R is within a range that is less than or equal to 43 and less than or equal to 48 at the upper boundary. We might be able to use a computer to see if there is a group of five different colors in the same graph. This task has more computing power than any other.
A graph with 43 connections has 902 edges. Either red or blue can be used. When rounded off, it is roughly 10272 possibilities. That's a 1 followed by a lot of zeros. It is assumed that the universe is made up of about 10 82 atoms.
A quintillion calculation steps per second is the amount of time it would take a calculating machine to perform a single calculation. The particles would have begun searching for a group of five in one second after the big bang. They would have had 3,600 4.35 x 10 17 seconds for this task so far. Only a tiny fraction of what is left to process would have been looked at by the atoms.
The mathematicians are trying to find a better solution to the problem. They have yet to find any.
Permission was granted for this article to be reproduced.