A data scientist at the Norwegian University of Science and Technology shows me a picture of a group of dots. The pattern is clear to a person. He says that the circle is obvious. This simple shape is likely to be difficult to recognize by an program. It misses the bigger picture.
There are many scientific processes. A computer's inability to see relationships is a problem for scientists. Data can be seen as dots floating in space. There are two numbers for latitude and longitude and a dot for a physical location. It is possible to plot genes in a mathematical space of many dimensions so that two genes with the same DNA sequence will be seen. Context affects the significance of a circular pattern. It is possible to show an evolutionary relationship between circles within genetic data and circles in a ship's position.
The data points in the sky are too complex to see with the naked eye. A set of instructions is needed to detect circles. Linear algebra is a type of mathematics used to study straight lines and flat planes. Researchers are turning to tda to find loops.
TDA is grounded in a branch of mathematics that studies stretchy shapes and is different from the simpler and rigid structures of linear algebra. The practitioners assume that all shapes are flexible.
The formation of constellations from stars is similar to the creation of revealing shapes from scattered dots. Researchers use the data points as joints in a virtual scaffolding to build complex structures that may extend through hundreds of dimensions. Much of the original data is contained in a more tangible form in the picture. They look for features that are still there even if the scaffolding is bent.
Topology can reveal qualitative, rather than quantitative, properties. There are aspects of the structure that persist even if there are errors. While noise jiggles the underlying data, it doesn't change the system's features. Robert Ghrist is a mathematician at the University of Pennsylvania. You need to use squishy math.
Scientists and mathematicians are working together to find unusual shapes in a vast range of data, representing anything from biological processes to the structure of drugs. Brain structure is perhaps the most intriguing of these investigations. The mathematicians have looked at how the brain responds to different stimuli. Some brain cells use a torus, the mathematical name for the surface of a doughnut, to map their environment, according to a new study.

Topologists are very careful to keep the number of holes in rubber sheets constant. They don't press closed an existing hole. A topologist can't tell the difference between a coffee cup and a doughnuts, because they both have a single hole.
The holes are classified according to their dimensions. The numeral 0 has a one-dimensional hole because it is formed by glueing together the ends of a one-dimensional line. A hollow ball can be created by starting with a two-dimensional plane and taping up the edges.
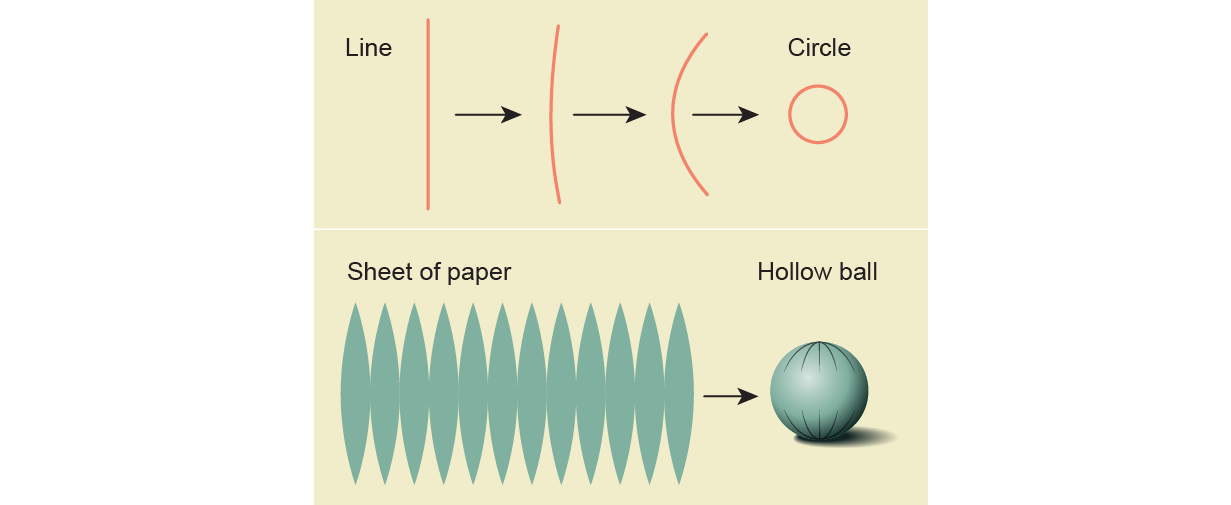
There are higher-dimensional holes in higher-dimensional shapes. A three-dimensional hole can be formed by closing up a three-dimensional space. Outside of most people's reach, this process can only be seen from a four-dimensional viewpoint.
A child can bounce on an inflatable ball that has multiple holes of different dimensions. The two-dimensional hole in the center of the ball is different from the one-dimensional hole in the handle. Topology is able to count holes in higher-dimensional shapes using many precise methods.
The brain is a huge transportation network according to a scientist. The infrastructure and roads are built from the connections between the brain and nervous system. The brain drives along these streets. It is possible to observe traffic patterns on top of the roads. As we move we can see traffic patterns changing.
A diagram of the brain may look like a collection of points. Some of them are connected by lines, and that's a sign of a connection. The structure is referred to as a graph by mathematicians. The structure of the brain is flattened by the graph, but it remains the same. There is a trade-off when creating a mathematical model.
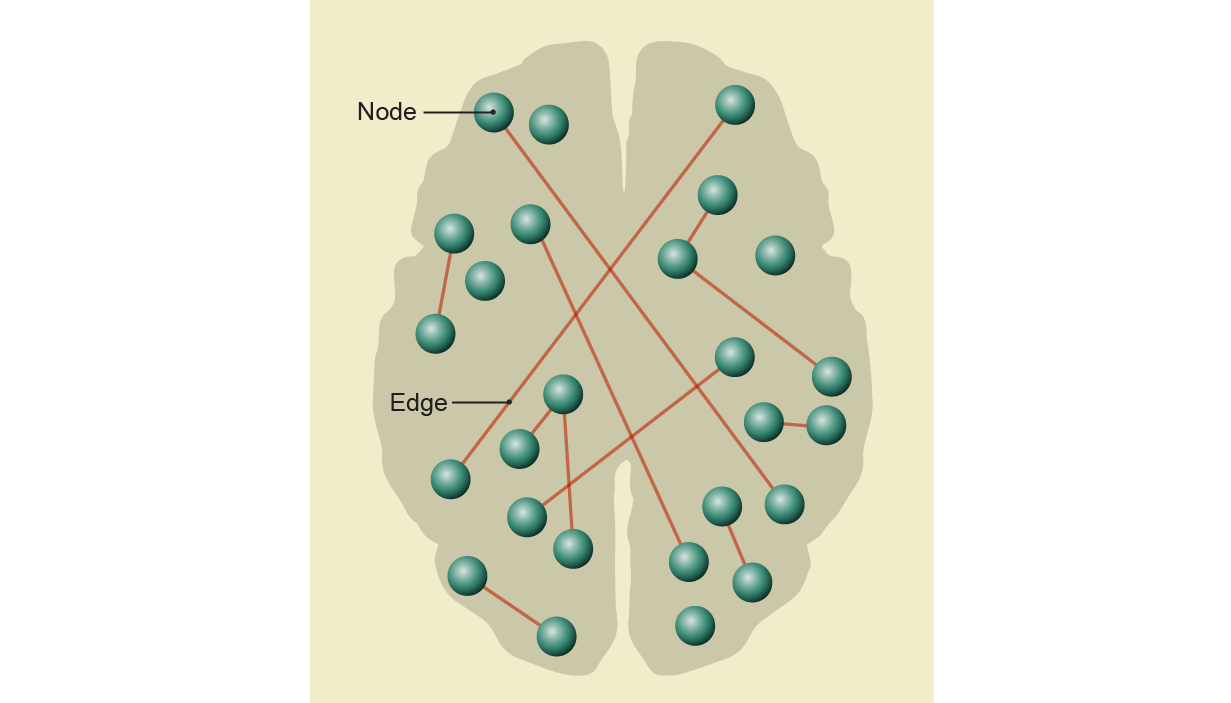
There is a mess in the graph of connections. She made the graph more complicated by doing something that was initially surprising. She analyzed the data from the Blue Brain Project, a simulation of the activity of a part of the brain involved in higher order functioning. There are representations of individual neurons in the computer model. Basic biological principles and experimental data from laboratory rodents determine when and how links will fire.
The brain's traffic patterns can be shown in a simulation. The simulation can be paused to give scientists a freeze frame showing which brain cells respond to a given stimuli. It's easy to make a graph out of this static image because it shows the data points and the lines between them. The simple graph was transformed into a voluminous shape by the work of Hess.
A complex is made from triangles. In the Blue Brain graph, there are three neurons with all three of them communicating. The mathematicians colored in a hollow triangle with a two-dimensional triangle to expand the structure into a simpler one. They filled in larger clusters of connected neurons. A three-dimensional pyramid with four faces would fill in a group of four brain cells.
The largest part of the complex was a seven-dimensional triangle because the maximum number of neurons that were observed firing was eight. There are many elements that overlap and form a multidimensional sculpture. A series of freeze frames were examined by the mathematicians and scientists. The maps were converted into a complex and analyzed how their shape changed in time.
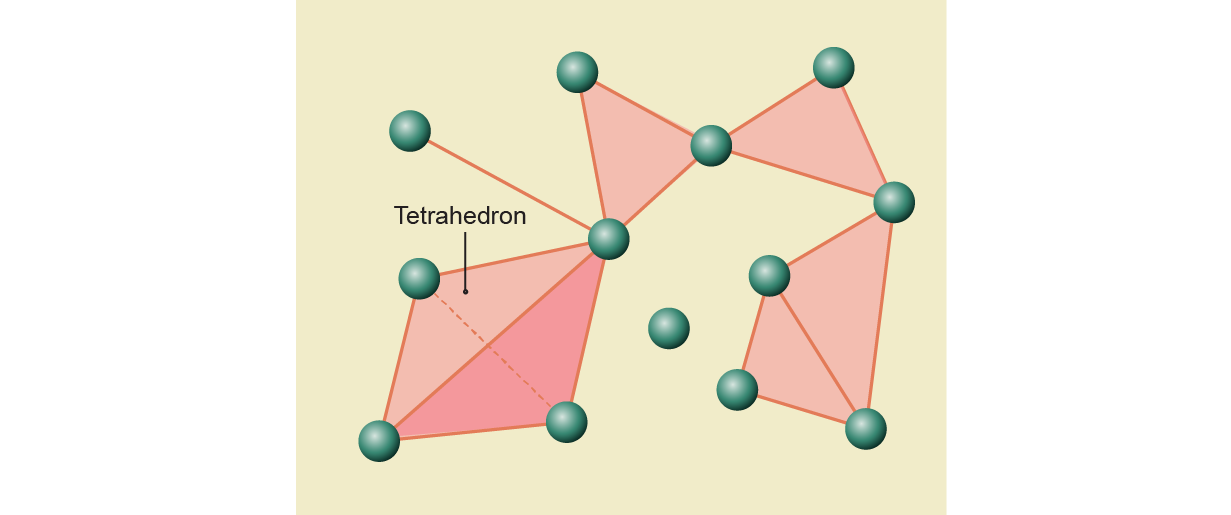
The simplicial complexes grew like Legos, adding in pieces of higher and higher dimensions until the sculpture reached the maximum of 3 or 4 dimensions. The whole thing vanished in a matter of moments. The structures are being created by theStimulus until it collapses.
A hollow circle is the same as a triangle because one can be bent into the other. There are holes in the seven-dimensional complexes that she and her co-workers built from the simulation of the brains of rodents. The number of holes went up as the shape grew. The structure contained a large number of two and three-dimensional holes at its peak. The pattern of holes showed a high level of organization in the brain.
Data can be represented by isolated points in an abstract mathematical space. The mathematicians have to figure out how to connect them. There are a lot of ways to link stars. Calculating implicit pictures is done using a technique called persistent homology. The essential features of the data cloud are analyzed by topologists.
They cast the widest net possible in order to form a dense mesh. A high-dimensional complex with few noticeable features can be filled in this web. The data needs to be connected at smaller scales to form this complex. Next, they narrowed the net to connect only nearby points. They use a sparser web to build a second complex. The mesh contains less data points than the simplicial complex. A group of smaller nets are used by the researchers. At every scale, there is a different snapshot of what that complex looks like.
There is a constellation with the same scattered data dots. The number of holes in each shape is studied by topologists. holes that persist through many different scales are of particular interest to them. The stubborn holes that survive through a range of scales point to the most important features of the data. A simple list of stubborn holes can be reduced to a complex mess with the help of TDA. Ghrist says that it's a way of paring down the data to the things that matter the most.
Sometimes the holes identified in this way have a different meaning. Periodic biological processes that repeat at regular intervals were found by a team of mathematicians and biologists. The metabolism of yeast or a mouse'sclock are examples. Referring or repetition is what it's called. "Perea, what do you think?" It should be like a loop in the space that you are looking at.
Researchers have been helped by TDA. These compounds can be found by changing the structure of drugs. The structure of a molecule is very complex and hard to analyze. To design novel drugs, computers need to work with simpler representations. A team from Michigan State University chose to reduce the number of molecules in their body. The collection of information gained through persistent homology is what this is about.
One type of neuron is the most basic level of brain organization. The discovery of place cells and grid cells, types of cells that are activated when an animal is in a specific location, was one of the reasons why John O'Keefe and May-Britt Moser were awarded the prize. A mathematician at Pennsylvania State University says that they act as sensors for position.
A rat's brain lights up when it is in multiple places. To figure out the relationship between the grid cells and the location of the rat, neuroscientists chose a single grid cell. A dot was drawn on a computer model of the floor to mark where the rat was when it activated. A pattern of dots emerged when the rat moved around the box. There were dots on the lattice that showed the locations of the grid cell. Each grid cell was marked in a different color. The grid cells had the same geometric pattern, but the dots were offset from each other.
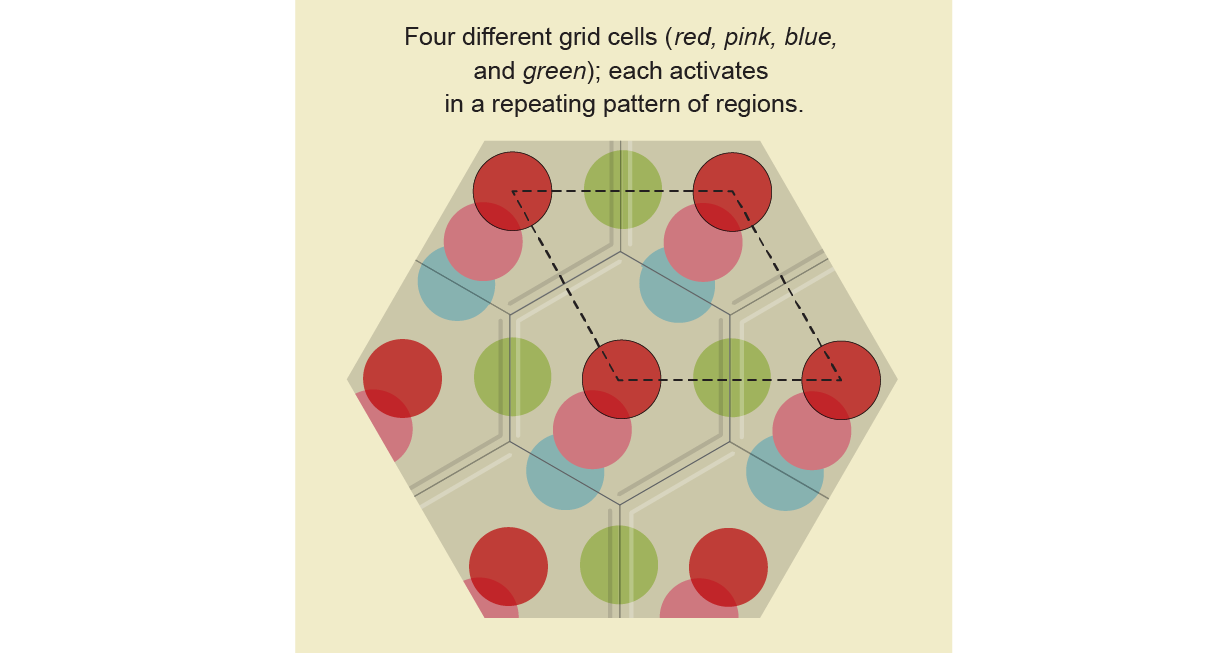
They were looking for the template that produced the hexagonal pattern to understand how the grid cells represented locations. Imagine a rubber stamp with cartoons on it. The line will be created when you roll out the stamp. There will be an image of Mickey Mouse on the line. The images came from the same spot. It's easy to roll out a stamp, but how do you make the template stamp from the pattern that you created is more difficult.
Four red dots formed the corners of a parallelogram when the rat was fired at. All the red dots of the same color correspond to a single cell. Topologists identified all the red dots and folded the parallelogram into a doughnut shape. They formed a cylinder with one on the top and one on the bottom of the parallelogram. They used glue to glue the two ends of the cylinder together. The four red corners of the parallelogram become a single point on the doughnuts. Every color has a dot on the torus. A torus is the correct map for how grid cells represent the floor of the box, just like the circular stamp was for the cartoons.
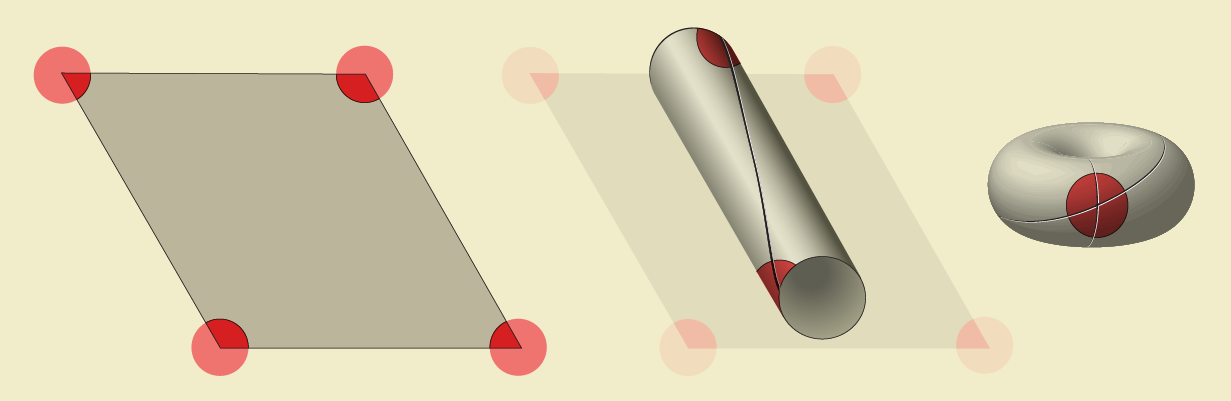
The rat ran around a box. When the rat moved around other test fields like a bicycle wheel, it was hard to see the pattern. Scientists were not confident about the underlying map of the grid cells. The arrangement of dots wasn't clearly planned.
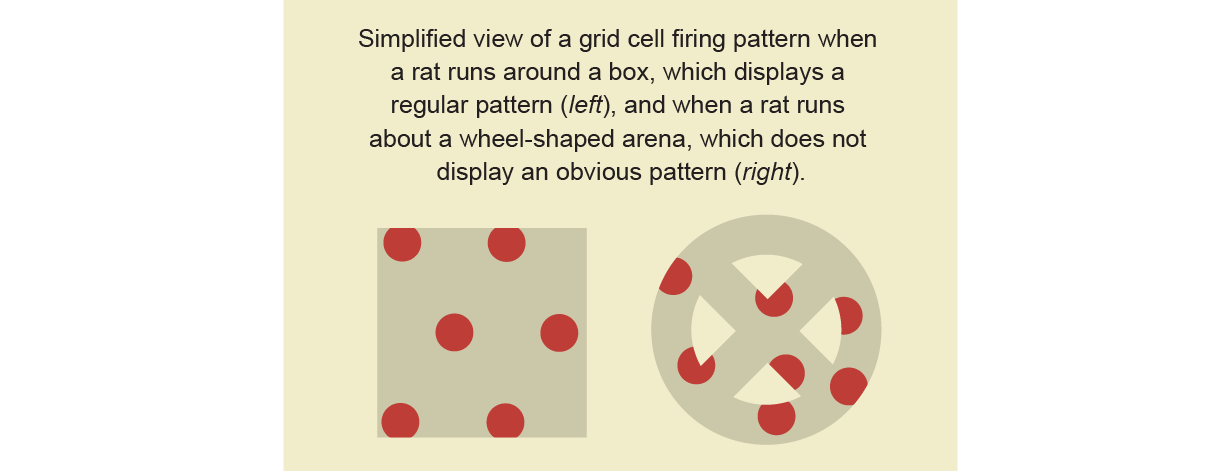
A team of mathematicians and neuroscientists, including Dunn, used grid cells to test a theory called continuous attractor networks, which predicts that certain neurons are wired together in a specific pattern. Researchers needed to determine if the grid cells always form a torus, no matter what environment the rat is in. They were looking for tori in the data.
The researchers studied the collective activity of all the grid cells instead of marking the positions in a box. They used a string of 0s and 1s to record the state of the network at regular intervals. The long string is in a very high-dimensional space. The researchers were recording the state of the system at different times. The data are too complex to be studied with the naked eye.
After using standard techniques to simplify the data, the team computed the persistent homology of the system by connecting the data points at different scales. The data formed a torus when the rat ran. The real test was when the rats ran around the arena. They were delighted that it formed a torus again.
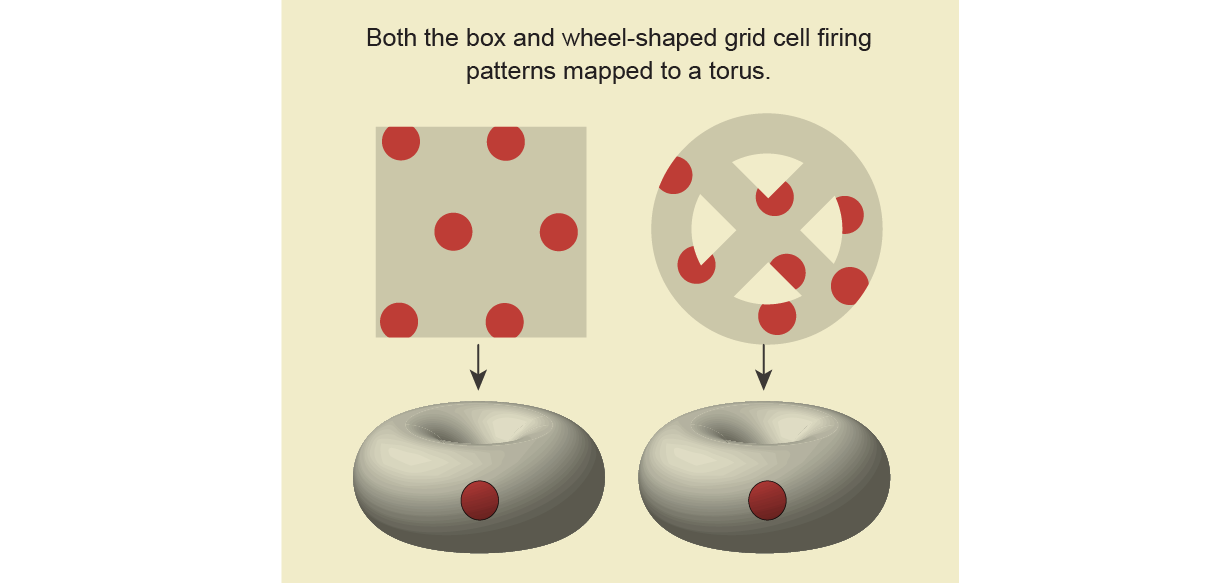
Researchers were able to collect data from a sleeping rat. The torus, a shape that persisted regardless of the rat's environment, supports the theory of continuous attractor networks. The shape of the grid cells seems to be related to the doughnut shape.
Powerful new computational tools allow many of these applications to be done. A mathematician at the University of Oxford says that none of this would have happened if people hadn't started building software. Nobody wants to use it if it isn't effective or if it doesn't scale well.
Thanks to these technologies, the uses of topology, which until recently seemed to be no more than a branch of mathematics, are growing. One of the pioneers of TDA says the applications are getting stronger. We have truly crossed the chasm.