There is a mathematical equation that could change medical procedures, natural gas extraction, and plastic packaging production in the future.
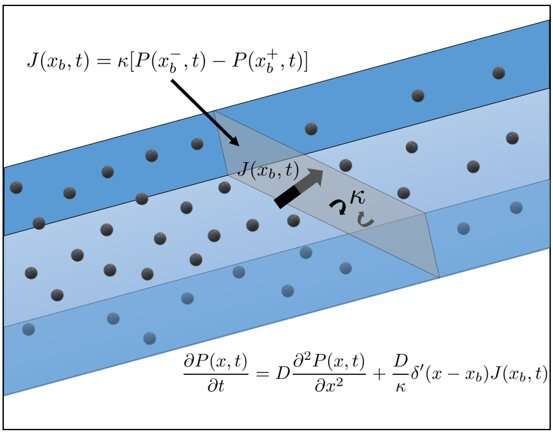
Scientists at the University of Bristol have developed an equation that can be used to model diffusive movement for the first time. It was 100 years ago that Albert Einstein and Marian von Smoluchowski created the first equation that represents motion for a wide range of entities.
Scientists looking at particle motion through porous materials have had to rely on approximations.
The findings, published today in the journal Physical Review Research, provide a novel technique that presents exciting opportunities in a variety of settings.
Toby Kay, the lead author, said that this marks a fundamental step forward. Through complex media of all scales, it is possible to model diffuse entities.
Attempts to represent movement through environments scattered with objects that impede motion have been limited. We are paving the way for exciting advances in many different sectors because we solved this problem.
The connection between different levels of description of a phenomenon is a form of creativity in mathematics. It was possible to find a new equation by zooming out to describe the process in a different way.
This mathematical tool can be used to improve products and services. Being able to model accurately the flow of water through biological tissue will lead to better interpretations of magnetic resonance scans. It could help to determine shelf life and risk of food poisoning. Evaluating the behavior of animals interacting with barriers such as fences and roads could help predict the consequences of climate change.
Over the past two decades, the tracking revolution has generated movement data of ever increasing quantity and quality. There is a need for more sophisticated modeling tools to represent the movement of wide-ranging entities in their environment.
The Associate Professor in Complexity Sciences at the University of Bristol said, "This new fundamental equation is an example of the importance of constructing tools and techniques to represent diffusion when space is heterogeneous."
In 2020 there will be a resolution to describe random movement in confined space. The mathematics of movement has many exciting potential applications, thanks to the latest discovery, which is a further significant step forward in improving our understanding of motion.
More information: Toby Kay and Luca Giuggioli, Diffusion through permeable interfaces: Fundamental equations and their application to first-passage and local time statistics, Physical Review Research (2022). journals.aps.org/prresearch/ac … 9165d2cc3a57a416bdf4