Ingrid Fadelli is a writer for the website Phys.org.
A new area of physics is aimed at understanding and interpreting thermodynamic concepts away from equilibrium. Over the past few years, findings in these fields have made it possible to understand different types of processes.
Two researchers at the University of California, Berkeley, Adam Frim and Mike DeWeese, have recently carried out a theoretical study looking at the full space of cycles with a continuously changing bath temperature. Geometric methods were used to get their results in the paper. The geometric space of control is studied in order to understand the response of the systems.
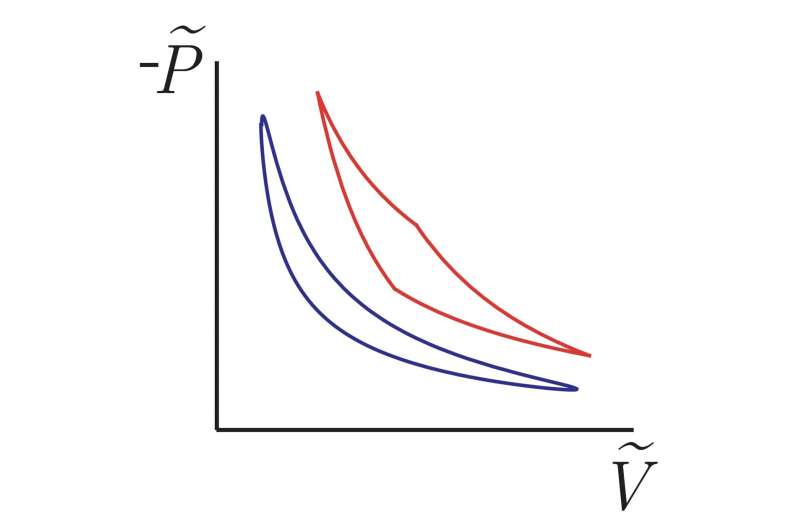
One coordinate in the space of control could correspond to the volume of the gas and the temperature. If an experimentalist were to turn those knobs, they would plot out a trajectory. The minimum dissipated energy of a given path is assigned to each curve.
Researchers can use thermodynamic geometry to look at interesting research questions, such as the best way to manipulate a given system, or build a classical or quantum heat engine.
The main goal of the paper was to figure out the most efficient way to run a tiny engine so that it produces the most useful work for the amount of fuel it uses. We were interested in constructing optimal closed curves that could function as highly efficient heat engines, instead of focusing on controlling the system with a set of initial and final settings.
Over a century ago, the main rules for understanding how to efficiently run large engines, such as those inside cars, when operated slowly, were first outlined. Frim and DeWeese extended their theories so that they could be applied to tiny engines. The engines are not in thermal equilibrium with the outside world and are affected by thermal fluctuations in the surrounding environment.
The area contained within the curve gives you the amount of useful work you get from one cycle of this. If you move very slowly around the cycle, the gas in the cylinder will stay close to the outside world. A small particle attached to a spring being buffeted by thermal fluctuations is an analogy to the P-V diagram.
Frim and DeWeese found that the amount of useful work provided by one cycle of the engine could still be thought of as a function of the area inside the closed curve. The length of the closed curve was found to be related to the amount of useful work that has been lost.
The result is relatively simple. The length goes through a process called thermosymetry. We thought about what the area inside the loop would look like if it were a closed loop. It turns out that the work output of the cycle is the same as the work output of a small length and large area.
The researchers were able to find optimal protocols that set a bound on the efficiency of all closed cycles. The design and development of efficient heat engines could be influenced by their findings. The implications of the bound on the efficiency of irreversible thermodynamic cycles set by this team of researchers is general.
DeWeese said that one of their goals was to develop the theory needed for engineers to design and build small and efficient engines. This could be an important area of technology. We want to understand the structure and function of the machines that are in the cells of all creatures and plants.
De Weese and Frim theorize that natural evolution may have picked for efficient machines. The rules they discovered could be a first step towards predicting the structure and function of machines in biology.
The interplay of lengths and areas of closed curves in geometric approaches to physics could have ramifications. The mathematical bound is more realistic than previous results that assumed the engine was very close to thermal equilibrium with the environment, but we still assume that the system is being driven slowly. Extending our results beyond this regime is something we are interested in.
More information: Adam G. Frim et al, Geometric Bound on the Efficiency of Irreversible Thermodynamic Cycles, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.128.230601 Journal information: Physical Review LettersThere is a science network.