There is a paper crane. A single square sheet of paper can be transformed into a bird, a dragon, or a flower by folding it. In the art of kirigami, strategically placed cuts can change the shape of the paper even further, creating complex structures from simple slit. An example of this is a pop-up book, where a different set of shapes emerge when the book is opened.
The game of what is possible is being changed by kirigami. Like with paper, repeated laser cutting of a sheet opens up the possibility for complex shape morphing powered by the opening and closing of slit. Because of the freedom available in designing slits, this creates a broad choice of geometries that can be used in a variety of ways. In real world applications, you might see a material like kirigami inspired that allows a robot to crawl, for example. Before these materials can be adapted for professional use, we need to better understand how kirigami materials shape-shift. The rules for simple building blocks are known, but the rules for their collective shape shifting interactions are not.
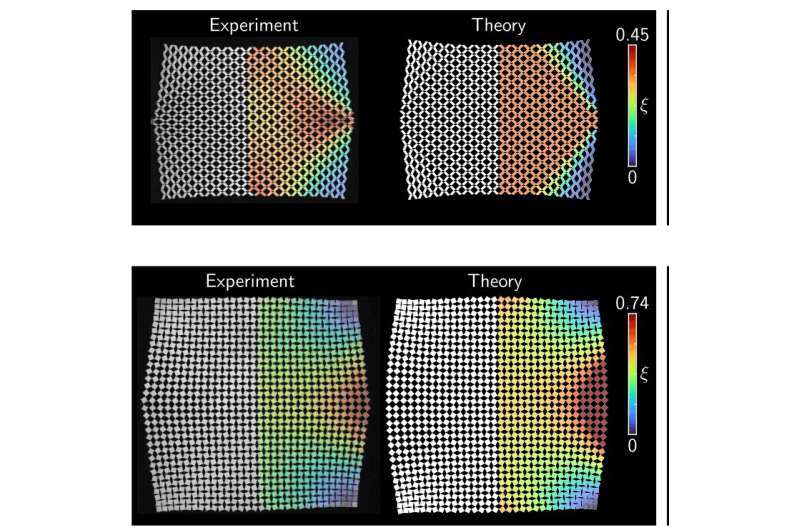
In a recent paper published in Physical Review Letters, a team of researchers from the University of Illinois at Chicago and the University of USC created a mathematical equation for predicting how kirigami inspired materials will move when pushed or pulled. The team includes USC Assistant Professor Paul Plucinsky, University of Illinois- Chicago Assistant Professor Ian Tobasco, and graduate student Imtiar Niloy.
According to Plucinsky, the geometry of these materials is not set straight. Rules about how you might choose architectures are needed. You need to be able to model the system so that you can predict how it will change when pushed or tugged.
Kirigami materials are not sensitive to the complicated geometry of their designs and do not apply to previous models of material behavior. When you introduce these patterns to loads, they produce a very non-uniform response.
When a material is cut, there are contained spaces that repeat in a pattern. In the case of kirigami materials, the cells can either be wave-like or decaying along elliptical arcs, depending on whether the pattern expands or contracts. Plucinsky said that a mathematical equation governs the behavior of things like water flow. A partial differential equation is the first piece of a bigger puzzle that Plucinsky and his team were able to develop.
The problem is a modeling one.
There is a modeling problem that is preventing the use of kirigami materials in the soft robotic, biomedical, and even space research arenas. There isn't much known about how kirigami materials work. If you don't have a good tool to model the systems in question, you would have a hard time investigating the design space and making predictions about the individual patterns.
Plucinsky and his team wondered if there was a simple mathematical equation that could be used to describe the materials. He said that the equation could be used to predict the behavior of the system.
The key to the equation was to realize that kirigami cells could be seen as atoms in a lattice, like in a conventional solid, where the units are the same and repeating. It was easy to derive an equation that reflected the changes in the physical structure of the material. If a moon rock lands on a kirigami-based space object, the equation shows how it would react.
There are puzzles of design.
One of the benefits of Kirigami patterns is that they are material independent. It's similar to the way in which they can create carefully engineered patterns with Additive Manufacturing. If you design the pattern correctly, the choice of material that you use doesn't have to be as important.
Plucinsky said that seeing the success of the mathematical model in predicting kirigami-inspired materials opens the door to using such modeling for other materials. If you have a repeating pattern, you can find an equation that is accurate. If you want to reverse engineer a property, you can say that it needs to feature an x-type pattern.
More information: Yue Zheng et al, Continuum Field Theory for the Deformations of Planar Kirigami, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.128.208003 Journal information: Physical Review Letters