Alignment of quantized levels in valleytronic materials

Researchers at the National University of Singapore have predicted that valley levels can be aligned at a critical magnetic field.

Many fields of science and engineering attempt to align distinct entities, such as two laser beams or two pillars. The creation of pseudo-spinors, which are useful for quantum computing applications, can be achieved by aligning quantized electronic levels.

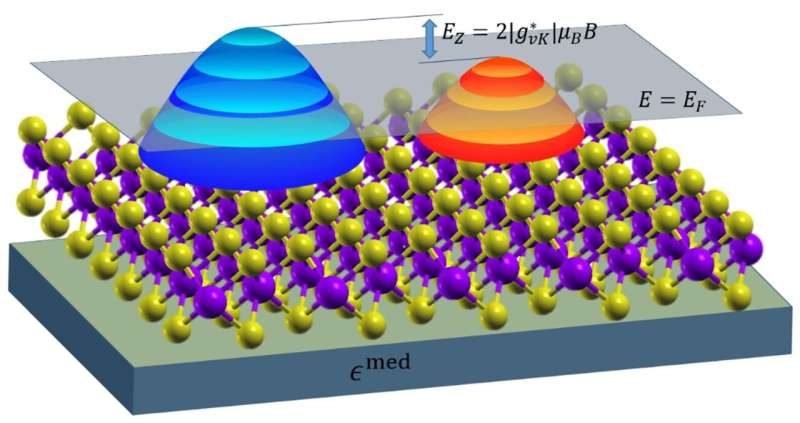
A magnetic field is applied to a 2D material The levels are known as Landau levels. There is particular interest in the levels of laure levels. Valleytronic materials can be used to control both the charge and spin of an electron. Charge carriers travel in opposite directions

An approach was developed to account for the effect of electron-electron interactions when predicting the energy levels in valleytronic materials. The effects of a magnetic field on the materials were amplified by these many body interactions. Computational results were found to be in agreement with experimental literature when applied to monolayer validation. The Landé g-factors are enhanced to quantify this amplification.

A change in the magnetic field caused a change in the population of charge carriers in each valley. The change in carrier population can't happen if the magnetic field is strong enough that all carriers are in the same valley. The alignment of the two valleys can be done with the help of the magnetic field.

The critical magnetic fields predicted are small so this effect can be realized in standard laboratories due to the large g-factors present.

The alignment of Landau levels predicted in this work is strong compared to previous proposals. Recent observations of fractional quantum Hall states in 2DWSe2 suggest the possibility of using Landau level alignment as a means to enable topological quantum computing applications.

More information: Fengyuan Xuan et al, Valley-filling instability and critical magnetic field for interaction-enhanced Zeeman response in doped WSe2 monolayers, npj Computational Materials (2021). DOI: 10.1038/s41524-021-00665-8